補足ノート「標準偏差の取り扱い〜「費用対満足度の風俗科学への導入について」の妥当性研究から〜」
by 元店長氏
1.はじめに
物事を統計的に処理するとき、「標準偏差」は非常に有用である。拙著「費用対満足度の風俗科学への導入について」について、サブちゃん氏が妥当性研究を論じ、それを評価指標として使用している。本ノートにおいては、論点を明確にするために標準偏差について整理する。
2.「真の値」は神しか知らない??統計学入り口
定規で10.1cmと計測された陰茎の長さ(ちょっと例が悪い・・・伸び縮みするかもしれないので)、もとい鉄の棒は果たして10.1cmなのであろうか?精密なはかりで45gと計測された睾丸の重さ、もといお気に入りのライターは真の値か?答えはノーである。そもそも「完璧な”真の値”」は神様しか知りえないのである。それは、ものを計測する行為自体に人間の過ちが含まれることが否めずかつ計測機器の誤差が含まれるからである。しかしながら、「確からしい値」は得ることができる。複数回計測しても同じ値であるときそれは「確からしい値」となり神しか知りえない「真の値」に近づくことができるのである。これを可能にするのが統計学である。ものづくりをするメーカーでは欠かすことのできない学問である。先に「人間の過ち」について言及したが、メーカーにおいて不良品を検出する際に「不良品でないものを不良品とする誤り」(あわてものの誤り)と「不良品であるものを見過ごす」(うっかりものの誤り)にまで分類するほど奥が深いものである(第1種、第2種の誤り)。これらも統計学の範疇である。
成績を表現する「SS」は、本ノートでのべる「標準偏差」と関わりが深い。果たして「標準偏差」とは何であろうか?それは、ばらつき具合を表現するものだ。
3.標準偏差と正規分布
能書きはたれているがあまり詳しくないので以後の説明にもどかしい部分があっても容赦いただきたい。軍資金として手に握るお金のうち1円玉の重さを無限大に計測すると次のような分布が得られることが統計学的に説明される(すみません。このへん、ようわかりません)
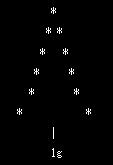
1円玉は1gとして作られているので上のような分布を示す。ここで、全ソープの値段を調べたとして次のような曲線を示したと考える。
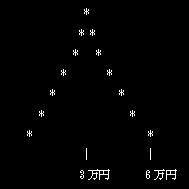
平均は3万円である。しかし、平均でばらつきは表せない。もしかすると、
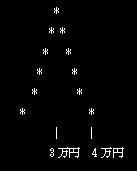
かもしれない。ばらつきはもちろん前者の方が大きいことは自明である。ここで標準偏差が大活躍する。
しかし、これは平均を囲むなだらかな曲線が正規分布であることが前提である。
正規分布の標準偏差はシグマ(σ)というもので表される。(計算式がきちんとあるが割愛。表計算ソフトにても計算可能)

算術的に導かれる「標準偏差」はばらつき具合を表しており、山がシャープならσ=1000円という数値になろう。具体的には次のことを意味する。
平均値(山のピーク)をuとした時、
u±σには、全母集団のうちの68%が入る可能性がある。
u±2σには、全母集団のうちの95%が入る可能性がある。
u±3σには、全母集団のうちの99.7%が入る可能性がある。
具体的に100件のソープ価格を調べ平均値u=30000円で標準偏差5000円の場合次のことが推察できる。
30000±5000円のソープは68件ある。
30000±10000円のソープは95件ある。
ソープの値段はほぼ30000±15000円で1件にも満たないお店が(0.3件)がこの範囲を超える。
サブちゃん氏の研究において、便宜的に60分コース単一のソープと仮定すると次のことが言える。
26034±8280円のソープは104件(153件中)ある。
26034±16560円のソープは145件(153件中)ある。
ソープの値段はほぼ26034±24840円で5件にも満たないお店が(4.59件)がこの範囲を超える。
4.おわりに
ばらつきを表す標準偏差であるが、実に難しい問題がある。果たして正規分布に従うのか?ばらつきが大きい場合には標準偏差でばらつきを表現してもごくあたりまえの結果しか導き出してくれない・・・。上記の例では、60分の単一コースとする時点で問題が生じる・・・。
サブちゃん氏も言及していたが「母集団」(統計対象)が小さいと意味をなさない。
著者は更なる風俗の定式化を模索中である。その際に用いるデータの統計学的根拠を明確にする必要性を執筆中に認識した。
風俗産業・経済研究室 主任研究員 元店長




