神は自然界をべき乗則で記述している。

　物理や数学を勉強すると避けて通れない「べき乗（累乗）」は、「同じ数字（文字）を複数回掛け合わせること」で、例えば、小中学校では、2乗（例：円の面積πr^2）だと平方、3乗(例：球の体積4πｒ^3/3)だと立方、と計算でならいます。

　車でブレーキを踏んでから停止するまでの距離は、走行速度の2乗に比例します。時速40kmと時速80kmでは、制動距離が4倍違います。
　ニュートンの万有引力の法則では、2つの物体の間には、物体の質量に比例し、2物体間の距離の2乗に反比例する引力が作用します。
　グーテンベルグ・リヒター則では、地震の規模が2倍になると、その頻度は1/4になります。従って、マグニチュードが１増すとエネルギーは10倍になるので、その発生頻度は1/100になります。100年に一度とか、1000年に１度とかの表現は、ここから来ています。
　このように、あらゆる自然現象が「べき乗則」で表現できます。

　物理現象だけではありません。
　人間の営みである経済活動も、べき乗則で表現できると言えます。
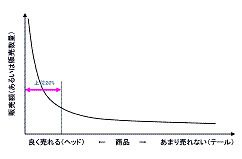
　商品の売上数量（売上金額）をグラフにプロットすると、べき乗則になっているのが判ります。経済分野では、これをパレートの法則（80対20の法則）とか、ロングテール理論とかで説明しています。

【グラフ１】販売数量をプロットした一般的な例

　先日、投稿者100撰を見ていて、何となく投稿本数の変化がこの商品の販売数量の変化に似ているなと思ったので、投稿者ごとに投稿本数をグラフにプロットしてみました。
　その結果が以下のグラフです。
　縦軸が投稿本数、横軸が投稿者です。4月下旬の投稿者100撰の本数と順番号200番までになっています。

【グラフ２】投稿者100撰から投稿本数グラフ

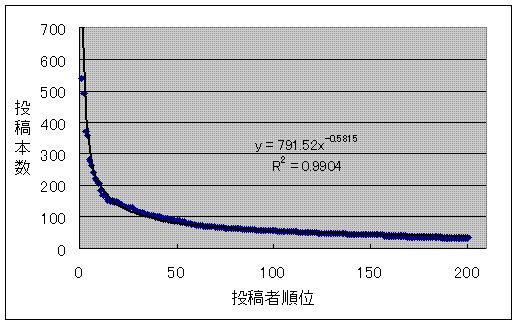
　思った通り、綺麗なべき乗曲線のグラフになっています。
　近似曲線の式は、「y=791.52x^-0.5815」となっています。R-2乗値が0.99ですので、きわめて適合していることになります。

　つまり、「日本ピンサロ研究会に投稿されているレポート数は、べき乗則に従っている」と結論できます。

　ではなぜ「べき乗則」になっているのでしょうか。
　それは「自然は曲線を創る（by湯川秀樹）」からです。

　以上、独断と偏見の上、乱文で申し訳ありませんが報告いたします。
　May a pinsalo be with you.

　研究部長　黒川洋介　(H23.05.16)